Formula

Drop a height $h$ from $I$ down to side $MT$. Then

$$\sin \theta = \frac{ h }{ r_{TI}\Delta t }$$

$$\sin \alpha = \frac{ h }{ r_{MI}\Delta t }$$

and so

$$\sin \theta \cdot r_{TI}\Delta t = \sin \alpha \cdot r_{MI}\Delta t \qquad \textrm{(Law of Sines)}$$

Through time the angles of the representation triangle are constant and the sides are proportional by some factor $\Delta t_{2}/\Delta t_{1}$: when solving for the angles, time may be eliminated from both the equation and the representation of the problem.

$$\sin \theta \cdot r_{TI} = \sin \alpha \cdot r_{MI}$$

Since point $I$ is not moving and thus $v_{T} = r_{TI}$ and $v_{M} = r_{MI}$, $\alpha$ can be expressed by the equation

$$\sin \alpha = \sin \theta \cdot \frac{ v_{T} }{ v_{M} }$$

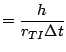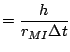Mathematically, the solution for $\alpha$ is ambiguous, since $\sin \alpha = \sin (180 - \alpha)$. However, in the physical situation it is clear that the $\alpha$ desired is always acute; otherwise $M$ would try and catch $T$ by running away from it rather than towards it--a sometimes successful but always inefficient strategy. (The two solutions for $\alpha$ are pictured in Figure 3; $\alpha_{1}$ is always preferable to $\alpha_{2}$, because a smaller $\alpha$ means $M$ is heading more directly towards the current location of $T$. Alternately: according the representation, a smaller $\alpha$ maximizes the length of $MT$, which represents $r_{MT}$, the closure rate between points $M$ and $T$.)

Figure 3: Ambiguous interception (mathematical representation).

Assuming the implementation of the $\arcsin$ function returns only the acute or right angle, the best solution for $\alpha$ can be simply stated

$$\alpha = \arcsin \left( \sin \theta \cdot \frac{ v_{T} }{ v_{M} } \right)$$ (1)